Par Super Neuro
Le titre est un peu alarmiste. Nous avons également écrit sur les ragots de Turing il y a quelques jours. Il ne fait aucun doute qu’il est considéré comme le « père de l’intelligence artificielle » par l’industrie.
L’aîné dont je parle aujourd’hui est également une figure remarquable : Shannon, que la communauté universitaire appelle respectueusement le « Père des sciences de l’information ». Comme nous le savons tous, la théorie de l’information a apporté de grandes contributions à l’industrie de l’intelligence artificielle, c’est pourquoi nous appelons Shannon « l’oncle de l’intelligence artificielle ».

Shannon était beau et confiant quand il était jeune, et il était également un parent éloigné de l'inventeur Edison
Le 30 avril 1916, Claude Shannon est né dans une petite ville appelée Gaylord, Michigan, États-Unis. À cette époque, Turing était loin, en Angleterre, et avait déjà quatre ans. Shannon a obtenu une licence en mathématiques et en génie électrique de l'Université du Michigan en 1936. En 1940, il a obtenu une maîtrise et un doctorat en mathématiques du MIT et a rejoint Bell Labs en 1941.
Comparée à celle de Turing, la vie de Shannon était plus douce. Il est décédé le 26 février 2001 à l'âge de 84 ans.
Le grand soutien de mon oncle à l’IA
La théorie de l’information, dont Shannon est le pionnier, est non seulement la pierre angulaire des sciences de l’information et de la communication, mais reste également la plus importante.Il s’agit d’une base théorique importante pour l’apprentissage en profondeur.
La théorie de l’information combine le calcul, la théorie des probabilités, les statistiques et d’autres disciplines, et joue un rôle très important dans l’apprentissage profond :
-
Fonctions de perte d'entropie croisée courantes ;
-
Construire un arbre de décision basé sur un gain d’information maximal ;
-
L'algorithme de Viterbi est largement utilisé en PNL et en parole ;
-
Les RNN sont couramment utilisés dans la traduction automatique et les encodeurs et décodeurs sont couramment utilisés dans divers types de modèles ;
Une brève histoire du développement de la théorie de l'information
Commençons par un exemple simple. Les deux phrases suivantes contiennent des quantités d’informations différentes.
"Bruno est un chien."
"Bruno est un gros chien brun."
Il est évident que les deux phrases transmettent des quantités d’informations différentes. Par rapport à la première phrase, la deuxième phrase contient plus d’informations. Il nous dit non seulement que Bruno est un chien, mais nous indique également la couleur du pelage et la forme du corps du chien.
Mais ces deux simples phrases ont été les plus grands casse-têtes pour les scientifiques et les ingénieurs du début du XXe siècle.
Ils voulaient quantifier les différences entre ces informations et les décrire mathématiquement.
Malheureusement, il n’existait pas à l’époque de méthode analytique ou mathématique facilement accessible pour y parvenir.
Depuis lors, les scientifiques cherchent la réponse à cette question, en espérant trouver la réponse à partir d’aspects tels que la sémantique des données. Mais il s’avère que de telles recherches ne servent à rien d’autre qu’à compliquer le problème.
Ce n'est que lorsque Shannon, mathématicien et ingénieur, a introduit « entropie »Après le concept. Le problème de la mesure quantitative de l’information a finalement été résolu, ce qui marque également le début de notre entrée dans « l’ère de l’information numérique ».
Shannon ne s'est pas concentré sur la sémantique des données, mais plutôt sur la distribution de probabilité et "Incertitude"Pour quantifier l'information et introduire "peu"Le concept de mesure de l'information.
Il estime que la sémantique des données n’est pas importante lorsqu’il s’agit du contenu de l’information.
Cette idée révolutionnaire a non seulement jeté les bases de la théorie de l’information, mais a également ouvert de nouvelles voies pour le développement de domaines tels que l’intelligence artificielle. Claude Shannon est donc également reconnu comme le père de l’ère de l’information.
Éléments communs à l'apprentissage profond : l'entropie
La théorie de l’information a de nombreux scénarios d’application. Nous examinons ici principalement ses quatre applications les plus courantes dans les domaines de l’apprentissage profond et de la science des données.
Entropie
Également connue sous le nom d’entropie d’information ou d’entropie de Shannon, elle est utilisée pour mesurer des résultats incertains. Nous pouvons le comprendre à travers les deux expériences suivantes :
-
Lancez une pièce de monnaie équitable, de sorte que la probabilité du résultat soit de 0,5 ;
-
Lancez une pièce biaisée de sorte que la probabilité du résultat soit de 0,99 ;
De toute évidence, il est plus facile de prédire les résultats de l’expérience 2 que ceux de l’expérience 1. Par conséquent, à en juger par les résultats, l’expérience 1 est plus incertaine que l’expérience 2, et l’entropie est spécifiquement utilisée pour mesurer cette incertitude.
Si les résultats expérimentaux présentent plus d’incertitude, alors leur entropie est plus élevée, et vice versa.
Dans une expérience déterministe où le résultat est complètement certain, l’entropie est nulle. Dans une expérience complètement aléatoire, comme un jeu de dés équitable, il y a beaucoup d'incertitude sur chaque résultat, donc l'entropie sera très grande.
Une autre façon de déterminer l’entropie est de définir l’entropie comme une fonction de l’information moyenne obtenue lors de l’observation des résultats d’une expérience aléatoire. Moins il y a de résultats, moins on observe d’informations et plus l’entropie est faible.
Par exemple, dans une expérience déterministe, nous connaissons toujours le résultat, donc aucune nouvelle information n’est obtenue en observant le résultat, et donc l’entropie est nulle.
Formule mathématique
Pour une variable aléatoire discrète X, les résultats possibles sont enregistrés comme x_1, ..., x_n, alors la formule de calcul de l'entropie est la suivante (l'entropie est représentée par H, bit unitaire) :
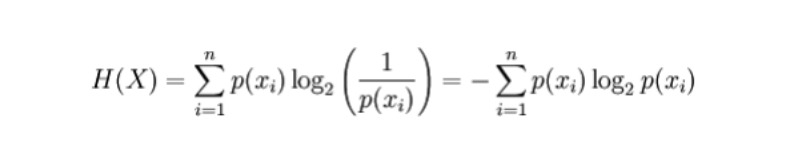
Où p(x_i) est la probabilité du résultat produit par la variable X.
application
-
Construisez un arbre de décision automatique. Au cours du processus de construction, toutes les sélections de fonctionnalités peuvent être effectuées à l’aide du critère d’entropie.
-
Plus l’entropie est grande, plus il y a d’informations et plus elles ont de valeur prédictive. Sur cette base, nous pouvons trouver le modèle le plus précieux, c’est-à-dire le modèle avec l’entropie la plus élevée, parmi les deux modèles concurrents.
Éléments communs et importants dans l'apprentissage profond : l'entropie croisée
entropie croisée
définition:L'entropie croisée est principalement utilisée pour mesurer la différence d'informations entre deux distributions de probabilité. Cela peut nous dire à quel point les deux probabilités sont similaires.
Formule mathématique
La formule de calcul de l'entropie croisée pour deux probabilités p et q définies dans le même échantillon est (l'entropie est représentée par H, bit unitaire) :
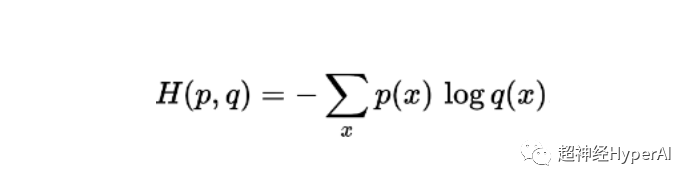
application
-
La fonction de perte d’entropie croisée est largement utilisée dans les modèles de classification tels que la régression logistique. Lorsque la prédiction s’écarte de la sortie réelle, la fonction de perte d’entropie croisée augmente.
-
Dans les architectures d'apprentissage en profondeur comme les CNN, la couche de sortie finale « softmax » utilise souvent une fonction de perte d'entropie croisée.
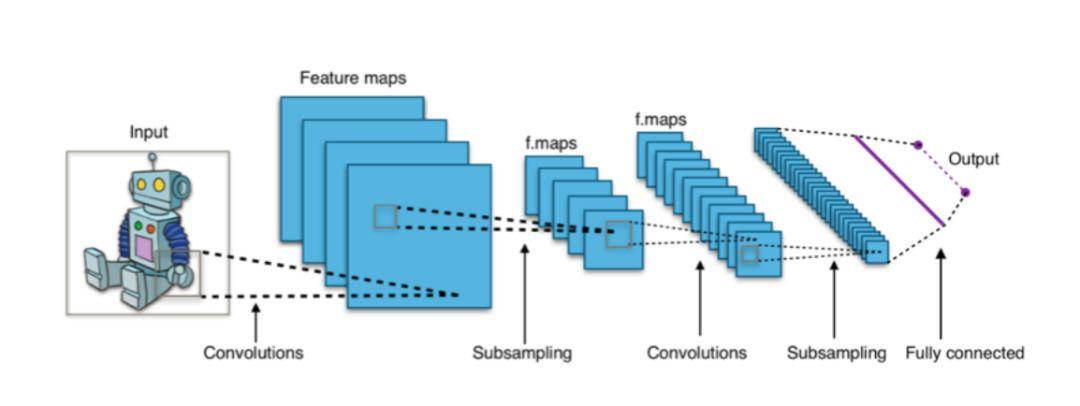
Figure 1 : Les classificateurs basés sur CNN utilisent généralement la couche softmax comme couche finale et utilisent la fonction de perte d'entropie croisée pour la formation.
Éléments communs et importants dans l'apprentissage profond : l'information mutuelle
Informations mutuelles
Définition L'information mutuelle est utilisée pour mesurer le degré de dépendance mutuelle entre deux distributions de probabilité ou variables aléatoires. En termes simples, il s’agit de la quantité d’informations qu’une variable contient.
La corrélation entre les variables aléatoires capturées par l’information mutuelle est différente de la corrélation générale qui est limitée au domaine linéaire. Il peut également capturer certaines informations non linéaires et dispose d'une gamme d'applications plus large.
Formule mathématique
La formule d'information mutuelle de deux variables aléatoires discrètes X et Y est :
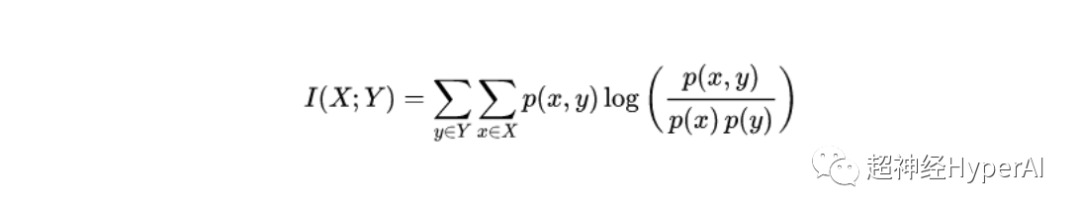
Où p(x,y) est la distribution de probabilité conjointe de x et y, et p(x) et p(y) sont les distributions de probabilité marginales de x et y, respectivement.
application
- Sélection des fonctionnalités : les informations mutuelles peuvent non seulement capturer la corrélation linéaire, mais également prêter attention à la corrélation non linéaire, ce qui rend la sélection des fonctionnalités plus complète et plus précise.
- Dans les réseaux bayésiens, l’information mutuelle est utilisée pour apprendre la structure des relations entre les variables aléatoires et définir la force de ces relations..
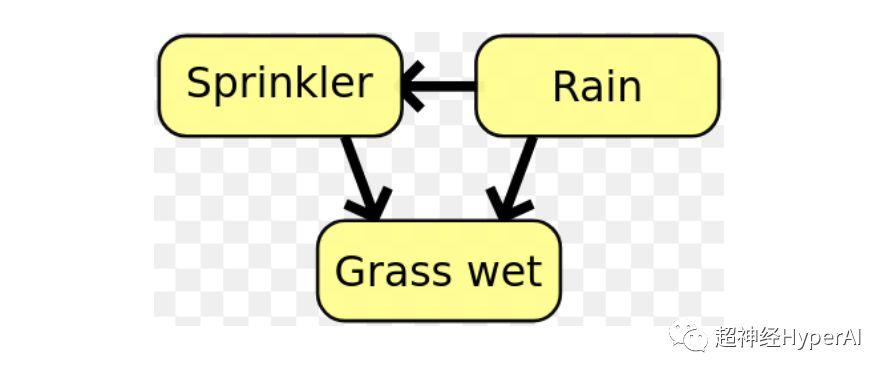
Figure 1 : Dans un réseau bayésien, la structure relationnelle entre les variables peut être déterminée à l’aide d’informations mutuelles.
Éléments communs et importants dans l'apprentissage profond : divergence KL
Divergence KL (divergence de Kullback–Leibler)
La divergence KL, également connue sous le nom d'entropie relative, est utilisée pour mesurer le degré d'écart entre deux distributions de probabilité.
Supposons que les données dont nous avons besoin soient dans la vraie distribution P, mais que nous ne connaissions pas ce P. Dans ce cas, nous pouvons créer une nouvelle distribution de probabilité Q pour s’adapter à la vraie distribution P.
Étant donné que les données de Q ne sont qu'approximatives de P, Q n'est pas aussi précis que P. Par conséquent, par rapport à P, certaines informations seront perdues dans Q, et la quantité de ces informations perdues est mesurée par la divergence KL.
La divergence KL nous indique la quantité d’informations que nous perdons lorsque nous décidons d’utiliser Q (une approximation de P). Plus la divergence KL est proche de zéro, plus les données de Q sont proches de P.
Formule mathématique
La formule mathématique de la divergence KL d'une distribution de probabilité Q avec une autre distribution de probabilité P est :
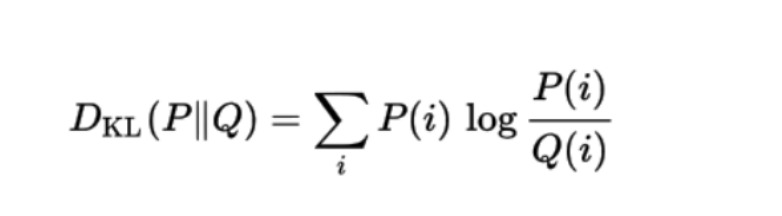
application
La divergence KL est actuellement utilisée dans le VAE (Variational Autoencoder) dans les systèmes d'apprentissage automatique non supervisés.
En 1948, Claude Shannon a officiellement proposé la « théorie de l'information » dans son article révolutionnaire « Une théorie mathématique de la communication », inaugurant une nouvelle ère. Aujourd’hui, la théorie de l’information est largement utilisée dans de nombreux domaines tels que l’apprentissage automatique, l’apprentissage en profondeur et la science des données.
Le premier prix Shannon
Comme nous le savons tous, la plus haute distinction dans l’industrie informatique est le prix Turing. Le prix Turing a été créé en 1966 par l'Association for Computing Machinery pour commémorer les contributions exceptionnelles de Turing. De même, le prix Shannon est tout aussi important dans le domaine de l’information.
La différence est que Turing est mort en 1954 et n’a pas eu l’occasion de savoir que le monde avait créé ce prix pour lui.
Shannon a eu beaucoup plus de chance. Le prix Shannon a été décerné par La société IEEE a été créée en 1972 pour honorer les scientifiques et les ingénieurs qui ont apporté des contributions exceptionnelles dans le domaine de la théorie de l'information. Lors de la première séance, Shannon lui-même a reçu le prix Shannon.

« Shannon a remporté le prix Shannon, et l'histoire l'appelle la routine Shannon »